Location: Mechanical Engineering, CMU, PA
Timeframe: Spring 2025
Introduction
This project investigates robust control design for a two-degree-of-freedom rotational system with coupled pitch and yaw dynamics. The Quanser Aero platform presents a challenging MIMO control problem due to strong cross-coupling between axes, actuator saturation limits (±25V), and significant plant uncertainty from parameter variations.
The objective was to design, simulate, and deploy controllers that track reference trajectories—a square wave (0.4 rad/s, π/6 amplitude) for pitch and sinusoid (0.5 rad/s, π/4 amplitude) for yaw—while maintaining robust stability and performance under model uncertainty. Four synthesis techniques were implemented and compared: H∞ loop shaping, H₂ optimal control, H∞ optimal control, and μ-synthesis.
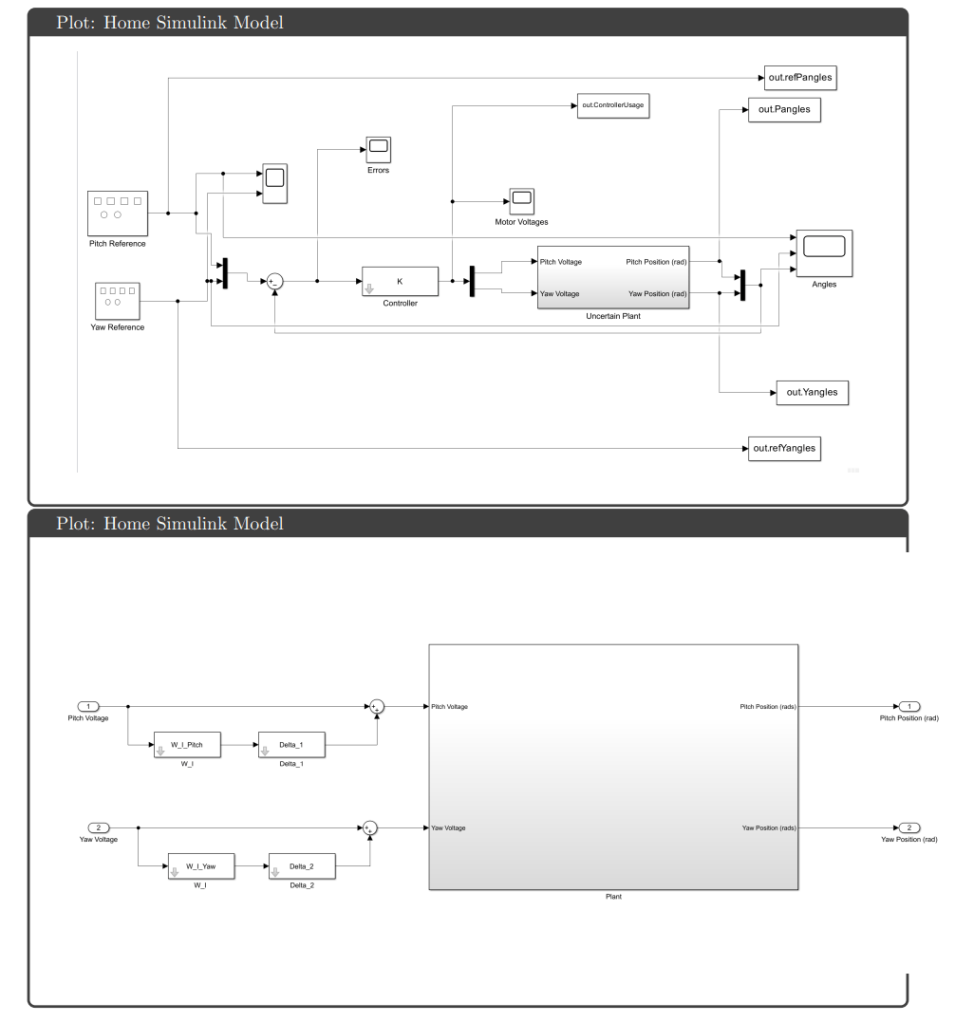
Design & Development
Team project. My role: Simulink modeling, controller tuning, and hardware implementation.
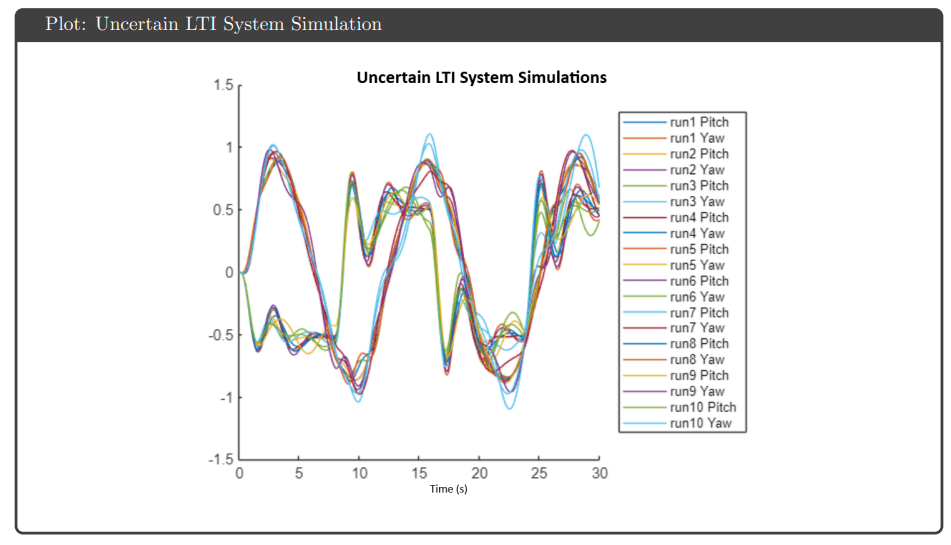
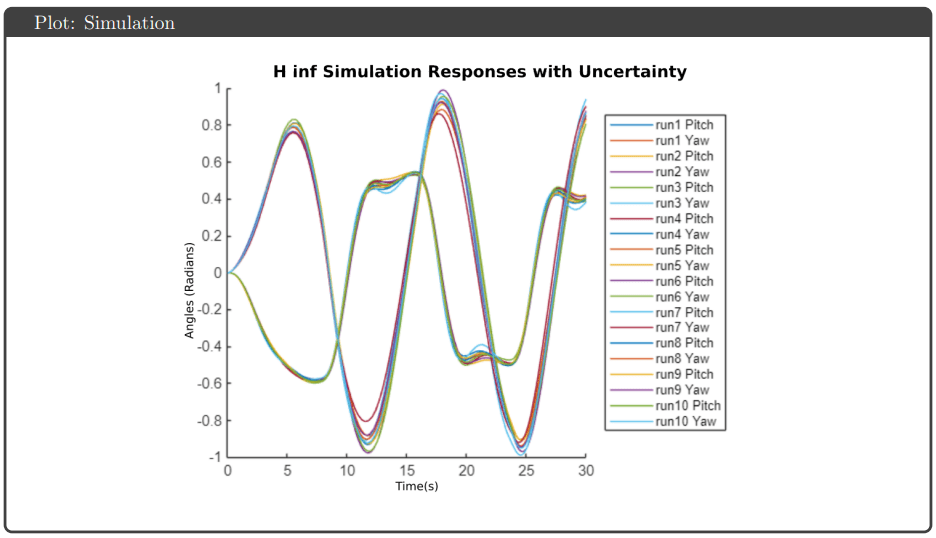
Uncertainty Modeling: Input multiplicative uncertainty weights were generated using the ucover command to bound plant variations across 100 sampled realizations. Separate weights for pitch and yaw channels captured frequency-dependent uncertainty, with higher uncertainty at high frequencies reflecting unmodeled dynamics.
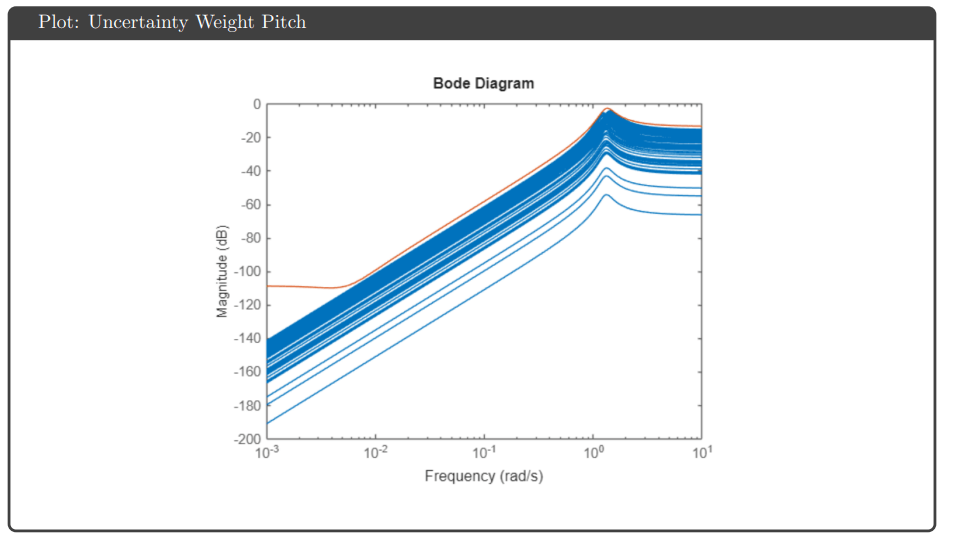
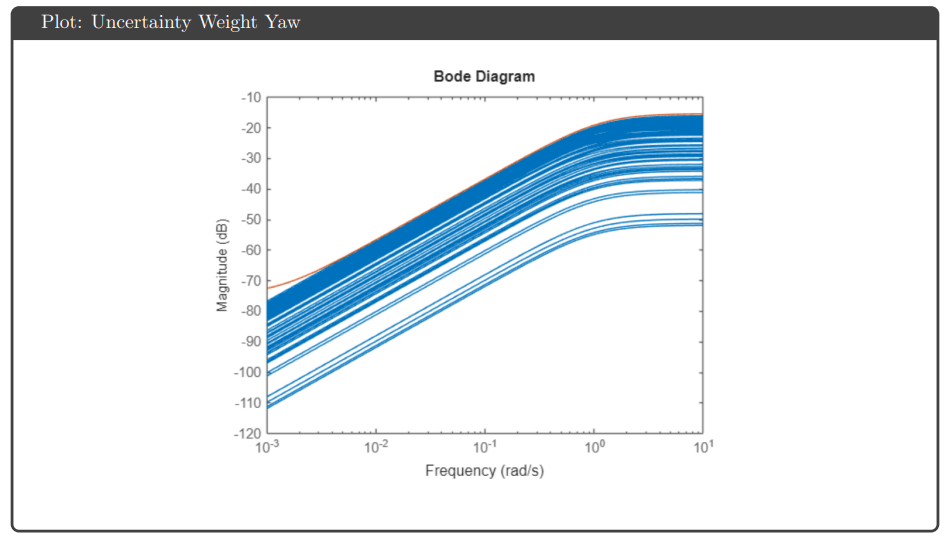
H∞ Loop Shaping: The Glover-McFarlane method (ncfsyn) shaped the loop transfer function to follow ω_c/s with crossover frequency tuned to 65 rad/s. This approach combines loop shaping intuition with robust stabilization guarantees from normalized coprime factor theory.
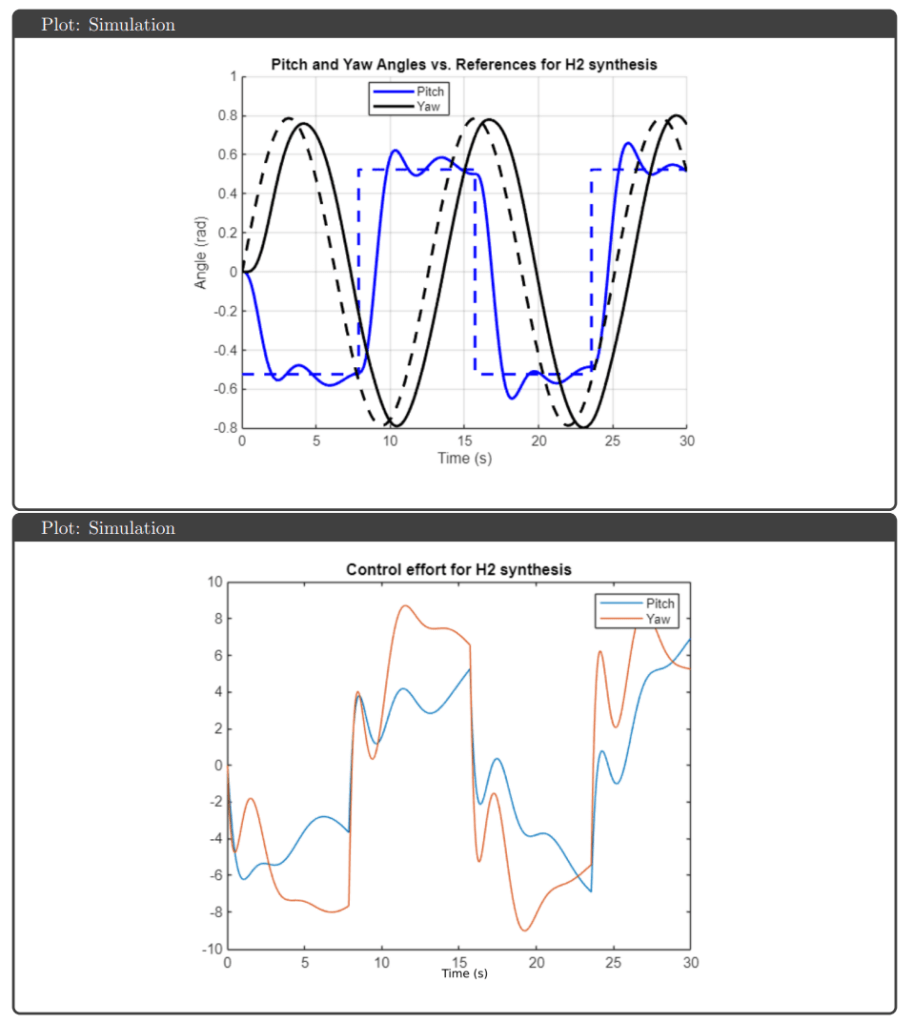
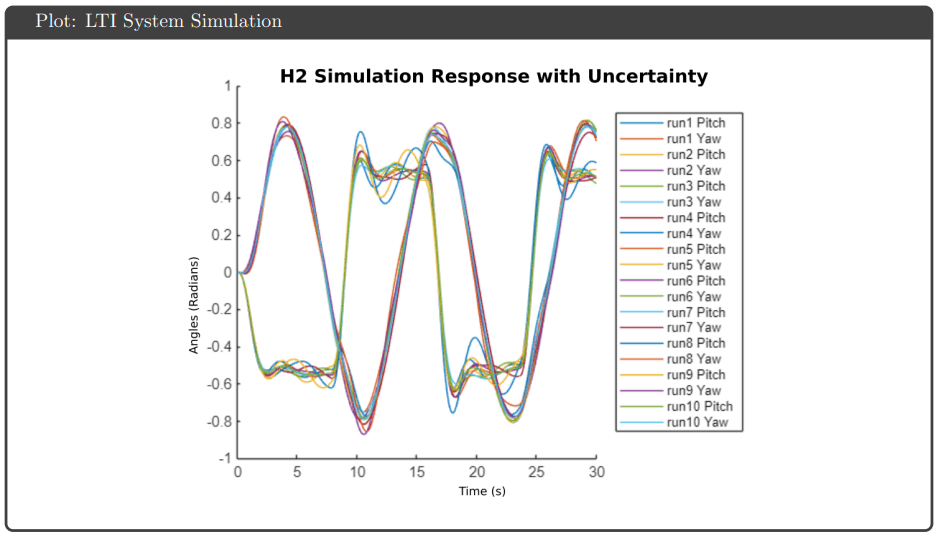
H₂ Optimal Control: A generalized plant was constructed with performance weight Wp (1000× DC disturbance rejection, sensitivity peak ≤3) and control weight Wu to prevent saturation. The h2syn command minimized the H₂ norm, optimizing average performance across frequency.
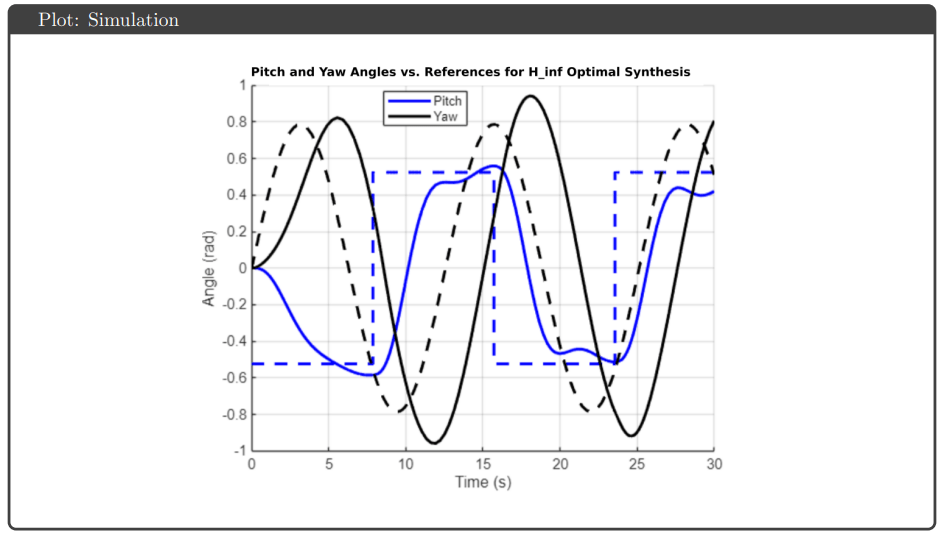
H∞ Optimal Control: The generalized plant incorporated uncertainty channels explicitly, enabling direct robust stability analysis. Bisection on crossover frequency achieved γ ≈ 1.05 using hinfsyn. The plant structure:
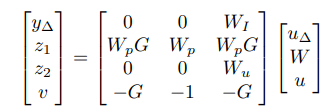

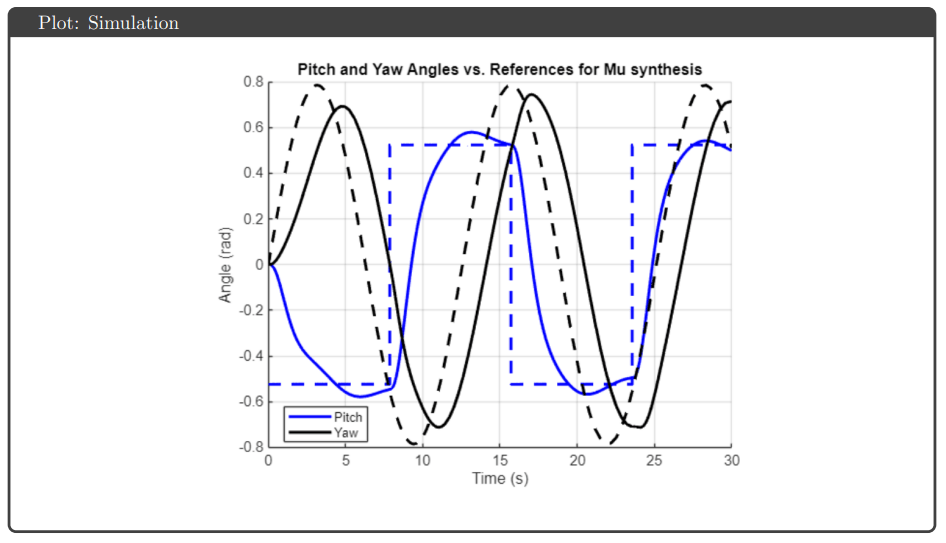
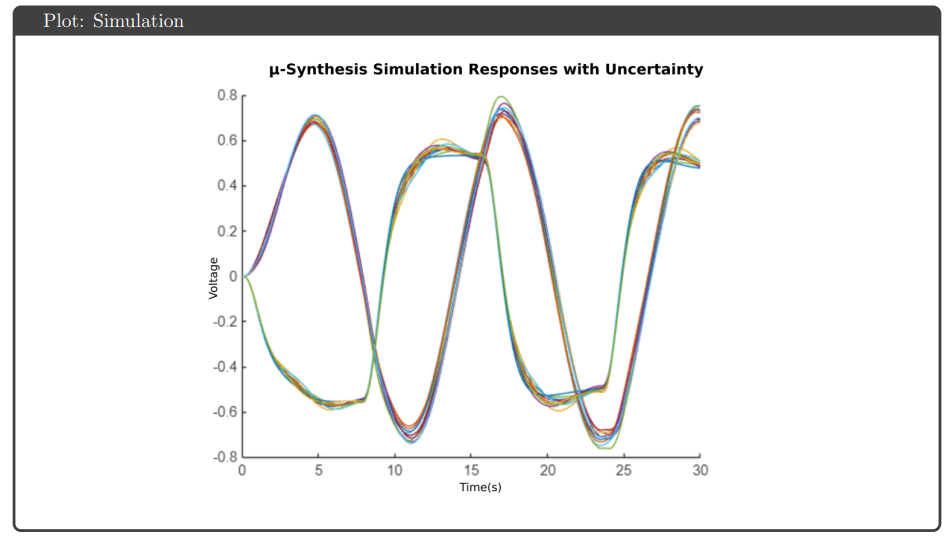
μ-Synthesis: Structured uncertainty was integrated directly into the synthesis using musyn, with model order reduction applied to match the H∞ controller complexity. This approach explicitly accounts for how uncertainty structure affects worst-case performance.
Challenges included tuning performance weights to balance tracking bandwidth against robustness margins, managing the coupling between pitch and yaw responses, and addressing hardware nonlinearities (actuator deadzones) not captured in the linear model.
Evaluation
Robustness Metrics Comparison:

Robust stability/performance guaranteed when value < 1. Hardware saturation refers to actuator voltage limits.
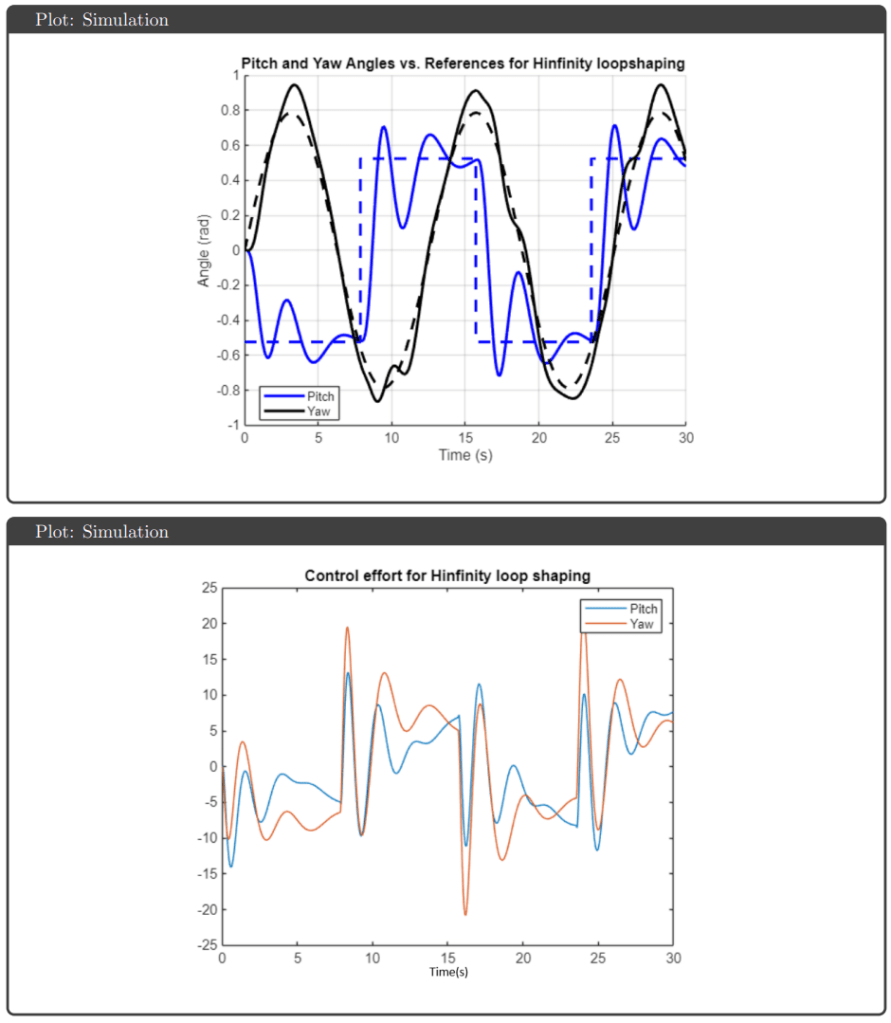
Simulation Results: All four controllers tracked pitch and yaw references well in simulation, avoiding actuator saturation under both nominal and uncertain plant conditions. The key differentiator was robustness guarantees: H∞ optimal and μ-synthesis achieved robust stability and performance metrics below 1, while H∞ loop shaping and H₂ optimal tracked effectively but failed to meet robustness thresholds.
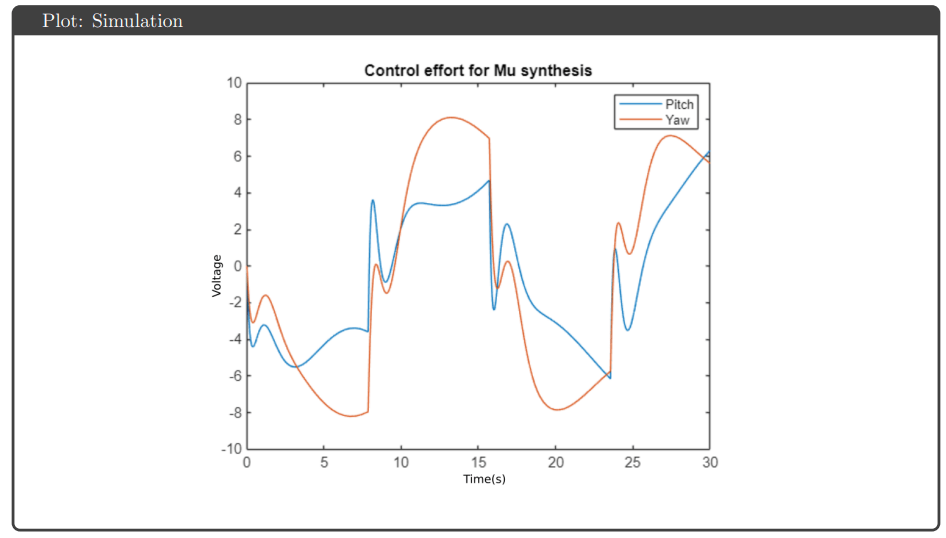
Hardware Results: Implementation on the physical Quanser Aero revealed performance gaps not predicted by simulation. All controllers exhibited response delays and overshoots attributed to actuator deadzones and discretization effects. The highly coupled dynamics caused pitch-yaw interaction—yaw overshoots triggered pitch compensation attempts and vice versa. Notably, H∞ optimal and μ-synthesis kept control effort below saturation limits, while H∞ loop shaping and H₂ optimal hit the ±25V actuator limits during operation.
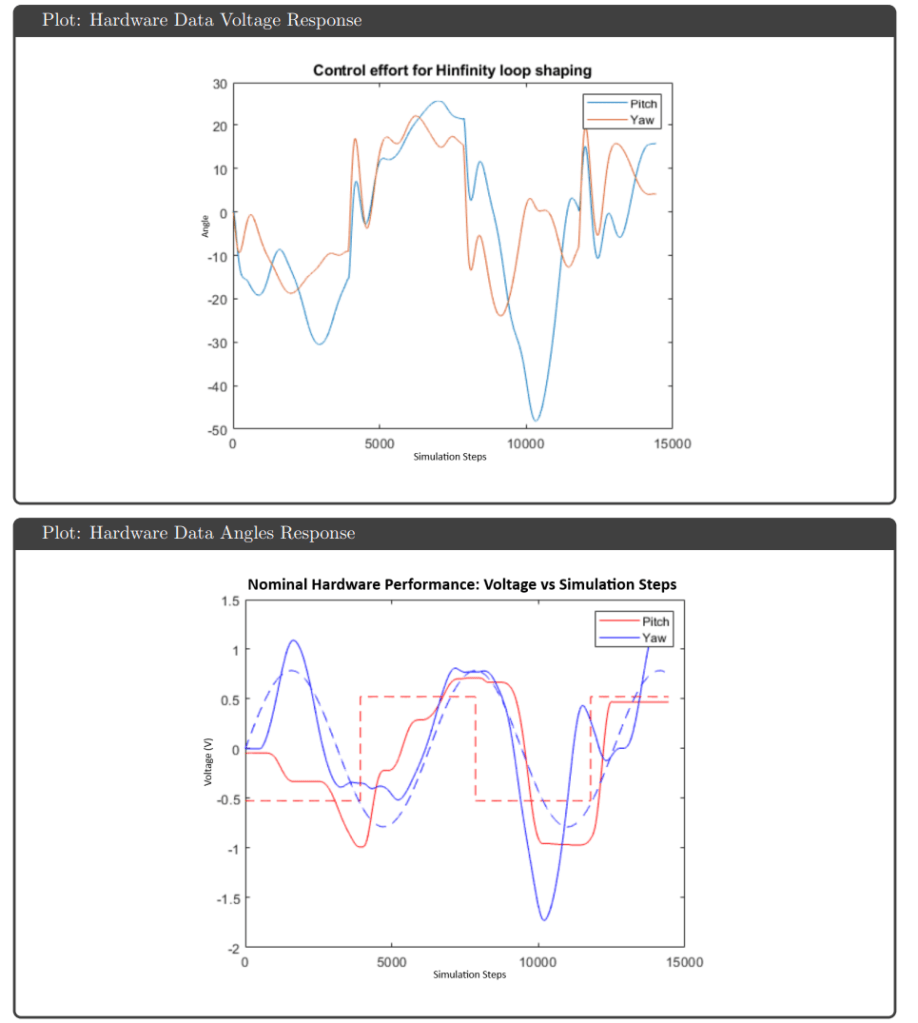
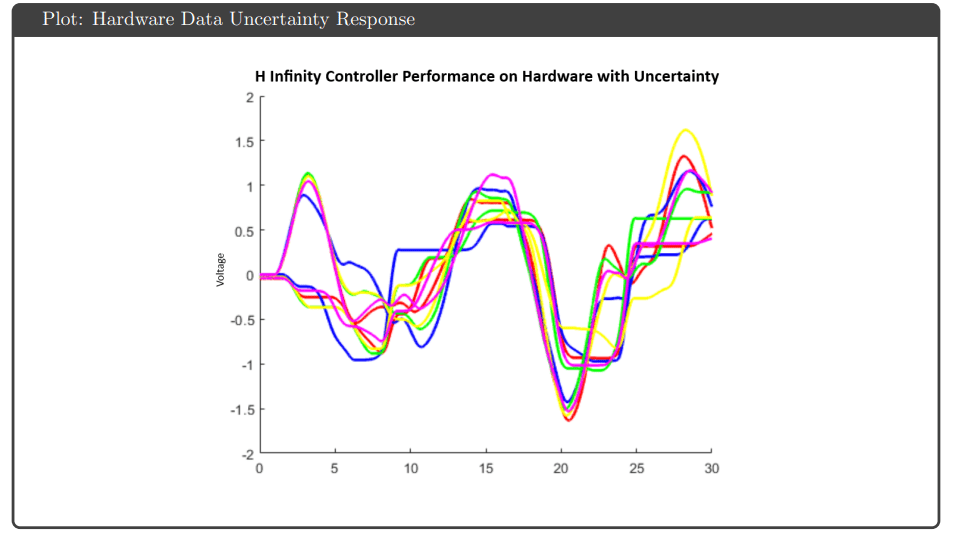
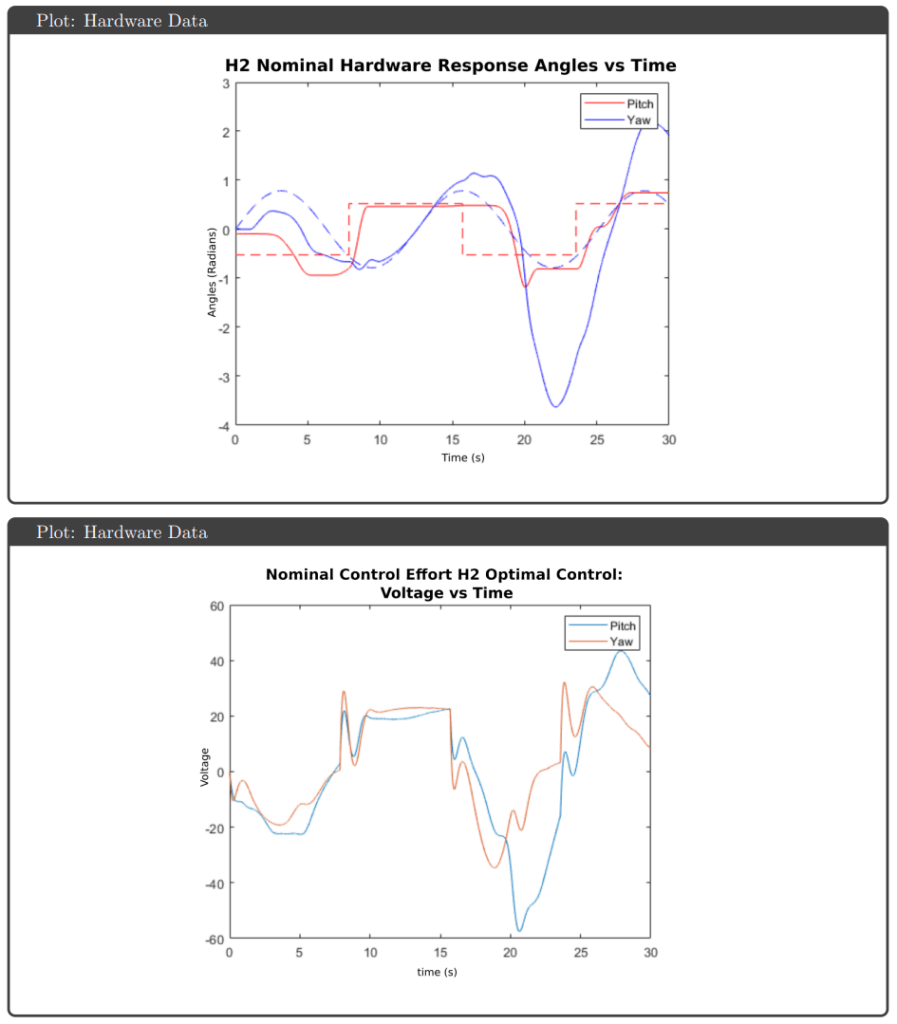
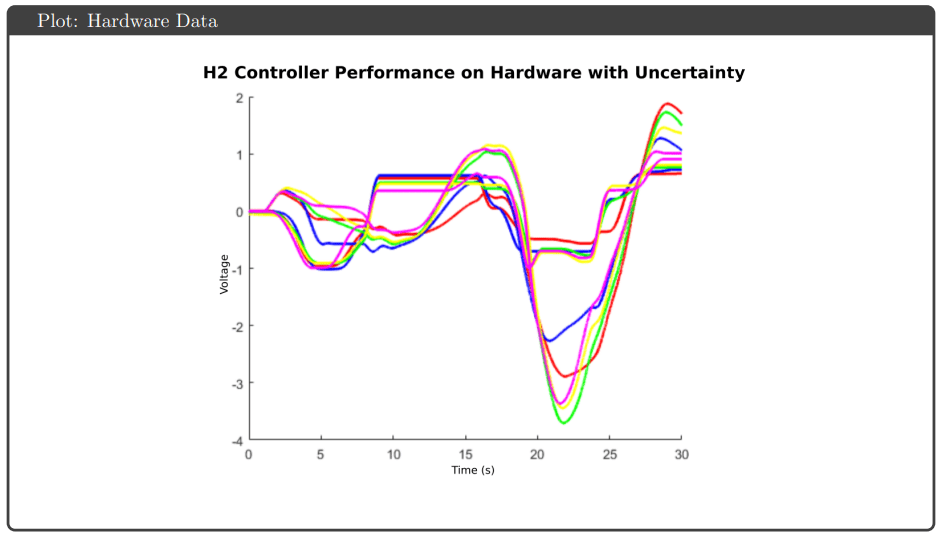
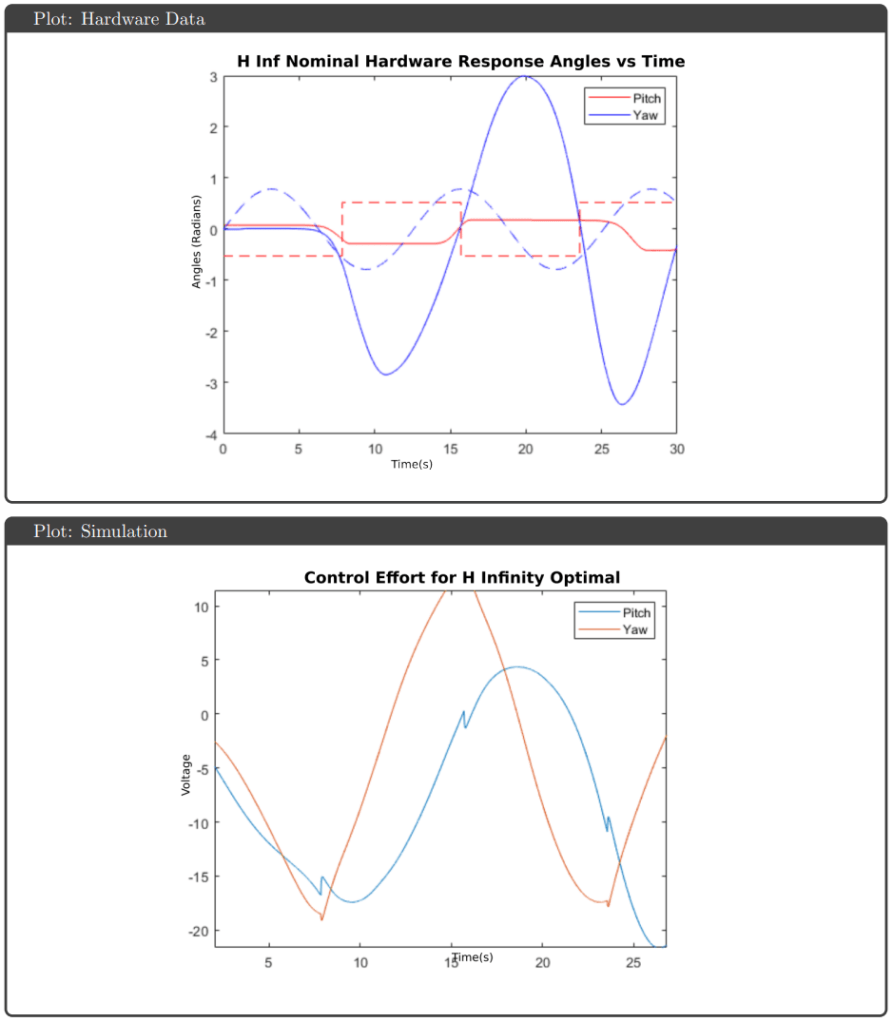
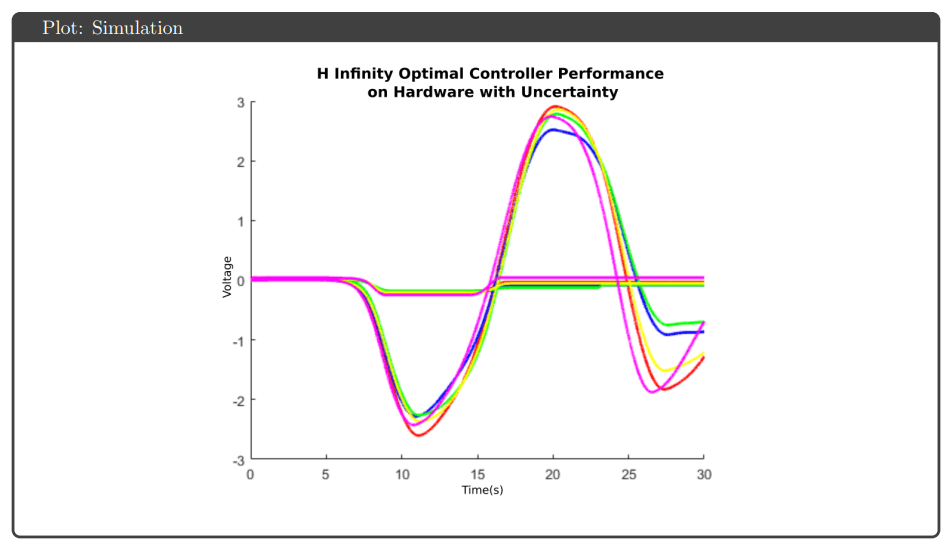
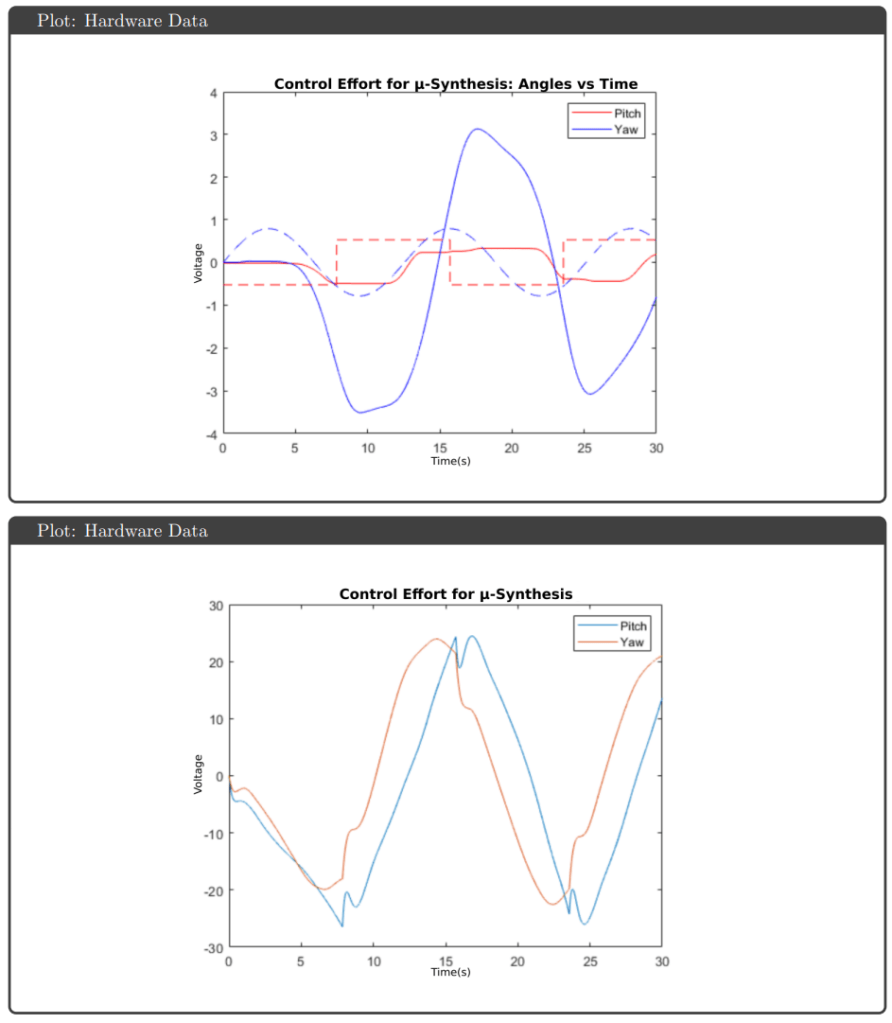

Key Observations: The controllers that achieved theoretical robustness guarantees (H∞ optimal and μ-synthesis) also avoided saturation on hardware, suggesting the robustness framework successfully accounted for gain variations that would otherwise drive actuators to limits. μ-synthesis provided the best robust performance metric (0.70) but required higher controller order, complicating tuning. The consistent sim-to-hardware gap across all controllers highlighted that actuator deadzones and other nonlinearities require explicit modeling beyond linear uncertainty bounds.
Conclusion
This project provided hands-on experience with modern robust control synthesis techniques, from uncertainty modeling through hardware deployment. Key learnings included constructing generalized plants with appropriate weighting functions, interpreting robustness metrics (robust stability margin, structured singular value), and understanding the tradeoffs between H₂ (average performance), H∞ (worst-case gain), and μ-synthesis (structured worst-case) approaches.
The results demonstrated that achieving robustness guarantees in simulation does not ensure equivalent hardware performance when significant nonlinearities exist. The project reinforced that controller complexity (order, bandwidth) must be balanced against practical implementation constraints. These robust control principles—modeling uncertainty explicitly, synthesizing controllers with guaranteed margins, validating on hardware—apply broadly to any system where parameter variations or unmodeled dynamics threaten stability and performance.
