Shot Optimizer

Location: Carnegie Mellon University, Mechanical Engineering (24-643 Optimization)
Timeframe: Fall 2024

Introduction

Golf strategy optimization has applications beyond recreation—the underlying mathematics applies to robotics trajectory planning, decision-making under uncertainty, and any domain where agents must optimize actions given inherent variability and environmental constraints. Understanding how to account for systematic biases in execution while maximizing expected outcomes is fundamental to autonomous system design.

The objective of this project was to determine optimal shot strategies for male amateur golfers approaching the green from 150 yards. Using strokes gained analysis—a metric that quantifies shot value based on distance to the hole and lie position (green, bunker, or rough)—we developed an optimization framework that accounts for a golfer’s inherent shot pattern tendencies, specifically whether they have a natural right or left lean in their shots. The goal was to find the optimal combination of club head speed, launch angle, and aim angle that maximizes expected strokes gained across various course configurations.

Strokes Gained Chart: Shows strokes gained/lost based on distance to hole and lie position (green, rough, bunker). Data from PGA Tour.

Design & Development

The system formulates golf shot optimization as a nonlinear programming (NLP) problem with three decision variables: club head speed (V_club), launch angle (θ_launch), and aim angle (θ_aim). My role focused on problem formulation, physics-based trajectory modeling, and optimization solver implementation.

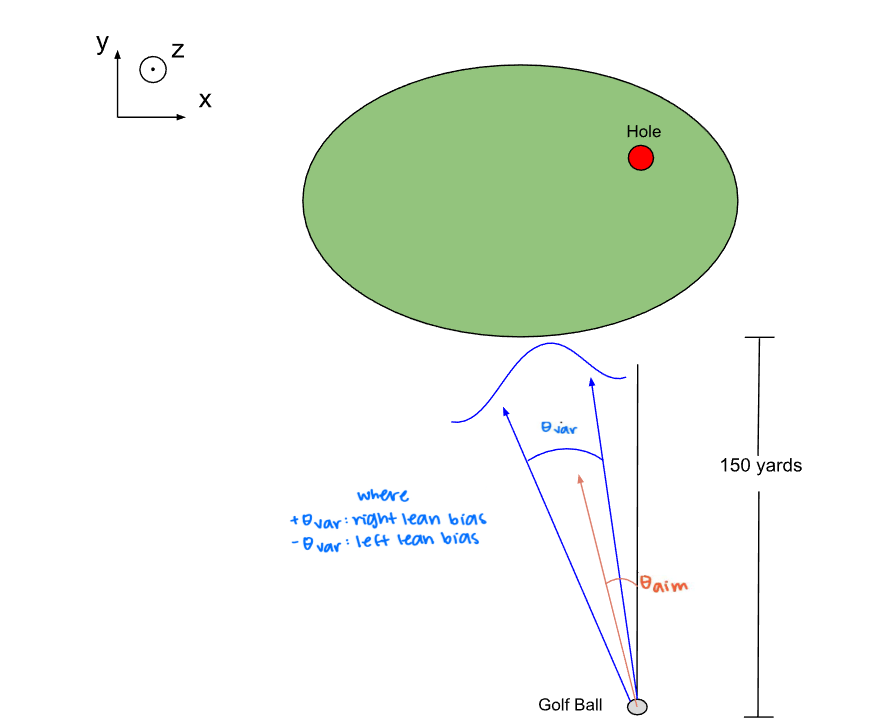
Physical Illustration: Top-down view (x-y plane) shows the green, hole position, aim angle (θ_aim), and shot variability (θ_var).

Key design elements included:

• Physics-Based Trajectory Model: Developed equations of motion incorporating aerodynamic drag to calculate ball landing coordinates. The model accounts for launch velocity decomposition, time of flight calculations, and coordinate transformations between golfer and absolute reference frames. Ball speed is derived from club speed using a smash factor of 1.32 based on PGA Tour data.

• Strokes Gained Function Construction: Created cubic spline interpolations through PGA Tour strokes gained data for three regions (green, rough, bunker). These helper functions are combined with golf course geometry to produce a single strokes gained function that takes landing coordinates and returns the expected strokes gained at that position.

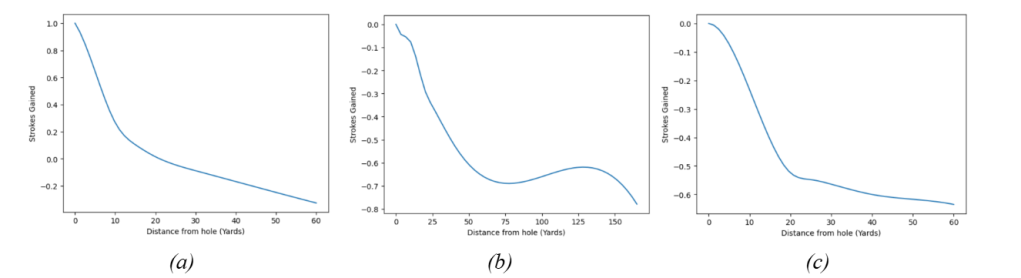
Cubic spline interpolations for strokes gained in Green (a), Rough (b), and Bunker (c).

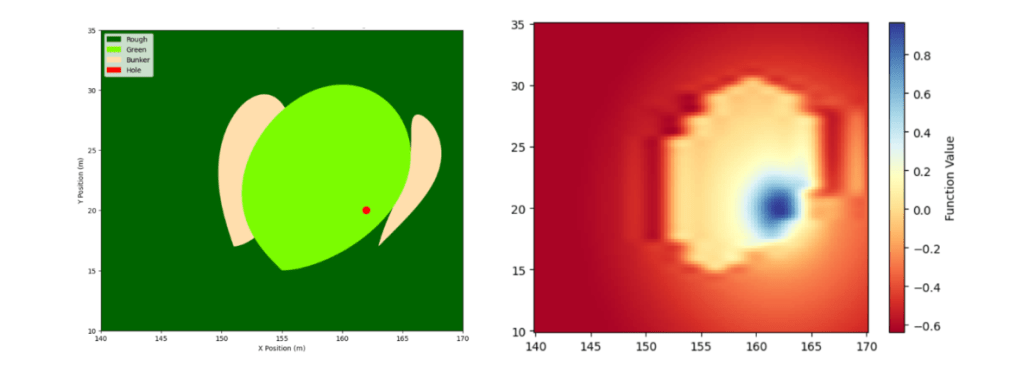
Base course configuration (left) with green, bunker, and hole; Strokes gained heatmap (right) showing highest values near the hole and lowest in bunker regions.

• Variability Modeling: Implemented shot dispersion through two stochastic parameters: θ_var (aim angle variability) sampled from a normal distribution centered at ±2° depending on golfer lean bias, and V_var (club speed variability) with standard deviation of 0.3 m/s. This creates a point cloud of possible landing positions for each intended shot.

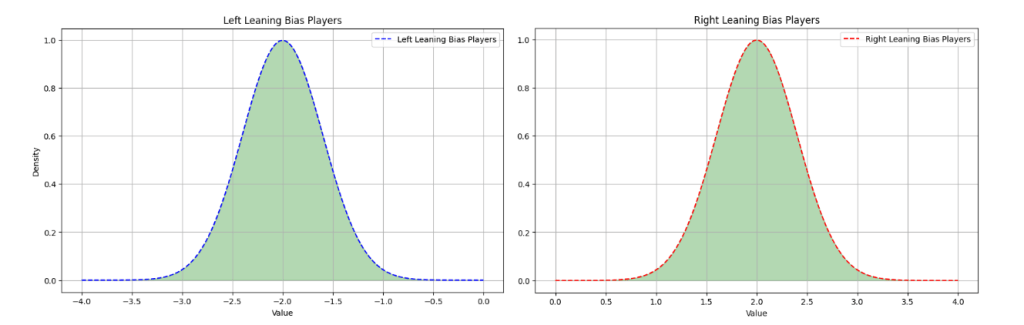
Shot Variability Distribution: Left-leaning players have θ_var centered at -2°, right-leaning players at +2°. This inherent bias affects where shots land relative to the aim point.

• Multi-Start Optimization: Used 15 randomly selected starting points with scipy’s trust-constr solver to handle the non-convex objective function. The expectation is approximated by averaging strokes gained over 2500 sampled shots (50 θ_var × 50 V_var combinations).

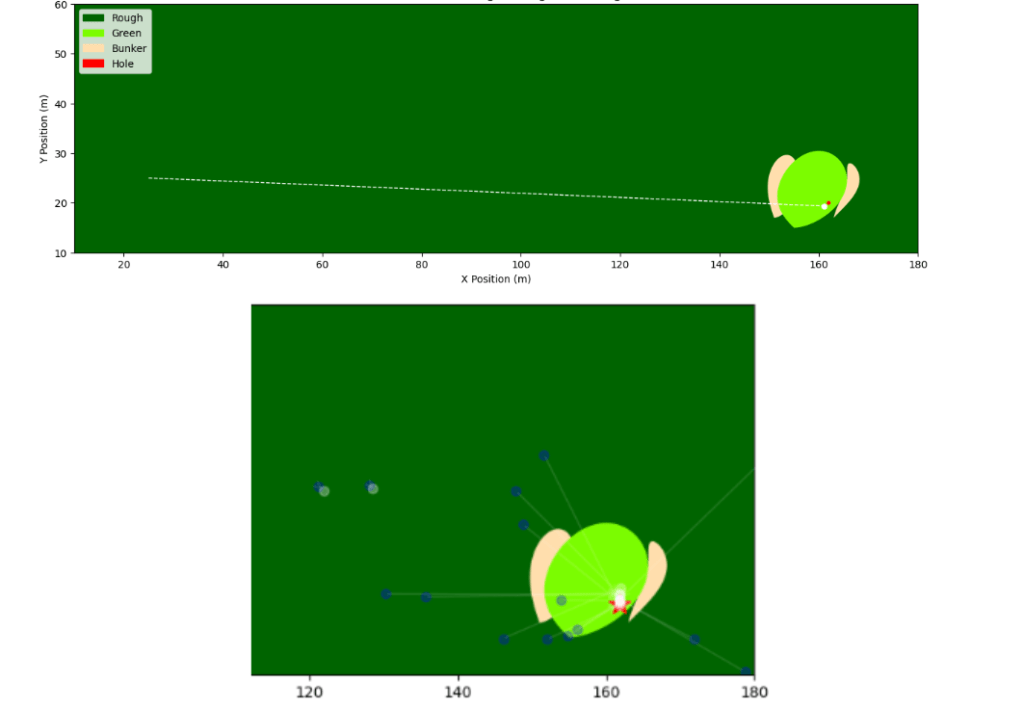
Multi-Start Optimization: Top shows full course with 150-yard shot trajectory. Bottom shows multistart approach—blue dots are random starting points, white dots are solutions from each starting point, red star marks the best solution.

Challenges I addressed:

• Constructing a smooth, differentiable strokes gained function from discrete PGA Tour data using cubic spline interpolation
• Handling non-convexity in the objective function caused by the strokes gained surface curving upward near bunkers and downward toward the green
• Ensuring solver convergence despite near-zero gradients in regions far from the hole, which caused gradient-based methods like SLSQP to stall
• Balancing computational cost of expectation approximation with solution accuracy

Evaluation

The optimization framework successfully converged to solutions across multiple course configurations for both left-leaning and right-leaning golfers. Key findings validated the approach:

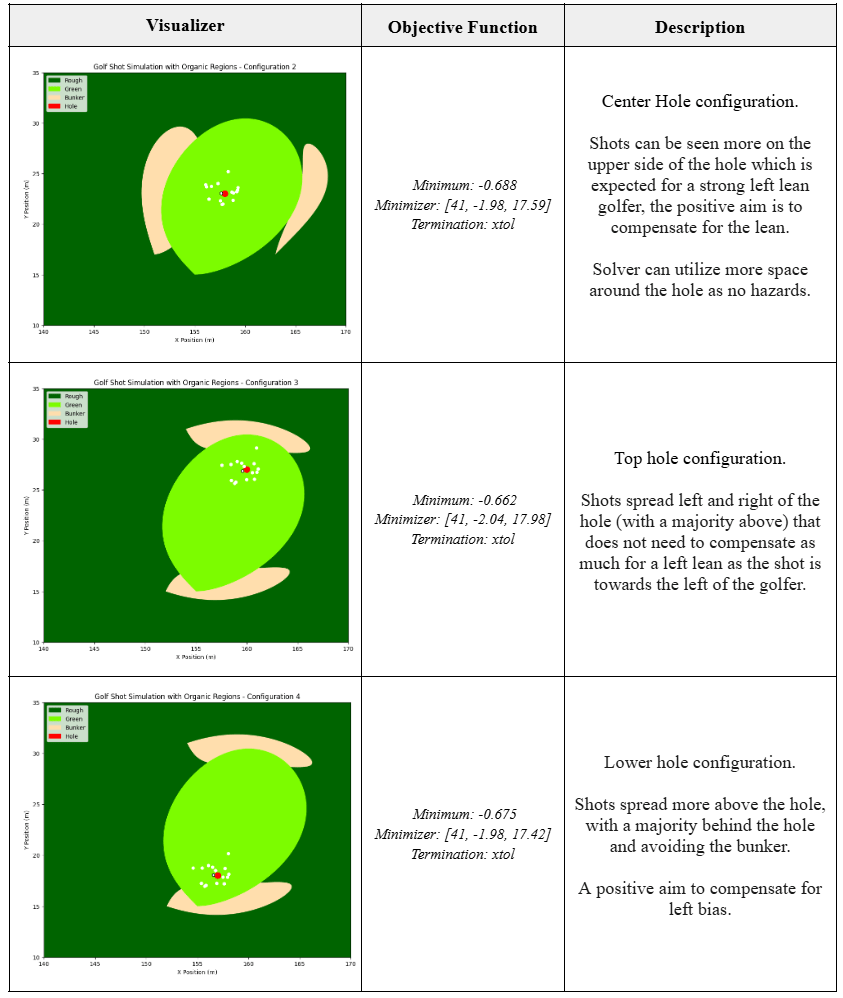
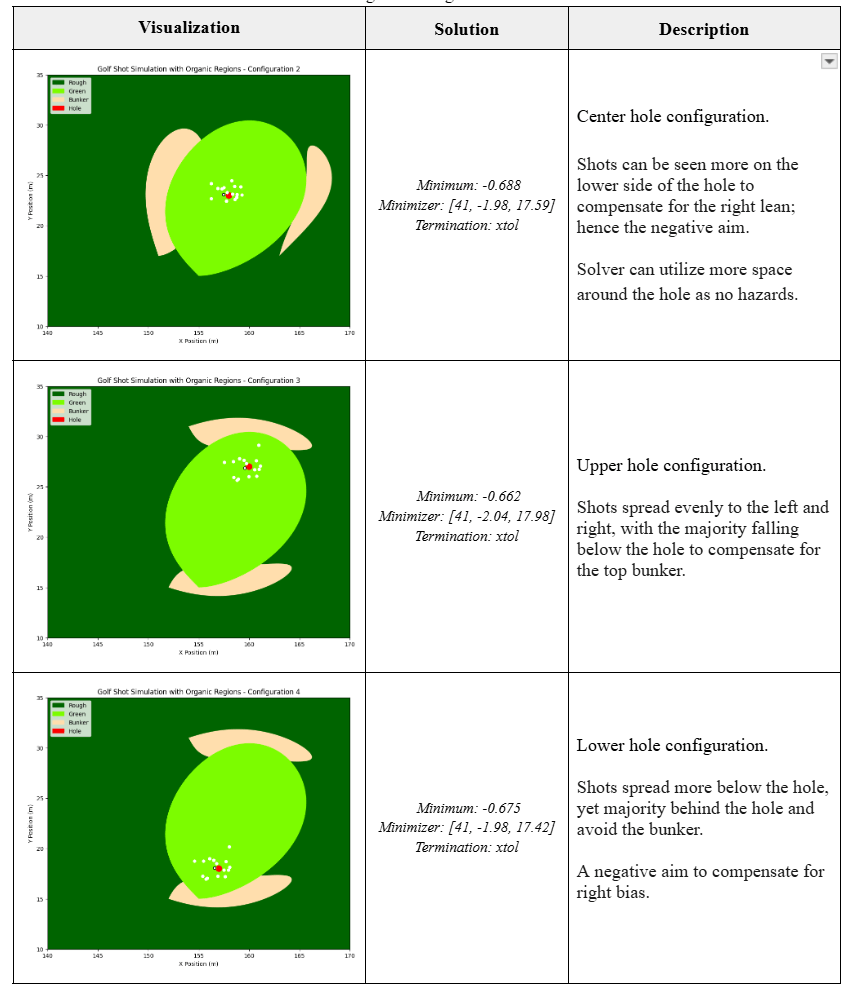
Optimization Results: Top shows left-leaning golfer solution (θ_aim = +2.11°, shots scattered right to compensate for leftward bias). Bottom shows right-leaning golfer solution (θ_aim = -2.03°, shots scattered left of hole to compensate for rightward bias). Black-bordered dot shows landing position without variance; colored dots show sampled shot dispersion.

Aim Angle Compensation: For right-leaning golfers, the optimal θ_aim was consistently negative (around -2°), compensating for the natural rightward bias. For left-leaning golfers, optimal θ_aim was positive (around +2°). This matches intuition—the solver learns to aim away from the bias direction.

Hazard Avoidance: When bunkers were positioned near the hole, the solver adjusted the aim angle to push shot dispersion away from hazards while still targeting the green. In edge cases with bunkers directly between the golfer and hole, the solver aimed away from the hole entirely to maximize expected strokes gained.

Constraint Activity: The club speed constraint was consistently active at its upper bound of 41 m/s across all configurations, with a Lagrange multiplier of 0.0081 strokes/(m/s). This indicates that allowing higher club speeds (e.g., using a 7-iron instead of 8-iron) would improve performance. Launch angle and aim angle constraints remained inactive, finding intermediate optimal values.

KKT Conditions Satisfied: The solutions satisfied all Karush-Kuhn-Tucker conditions—complementarity, feasibility, stationarity, and non-negativity of Lagrange multipliers—confirming local optimality. Given the single-hole objective, all local minima correspond to landing near the hole, making these solutions globally optimal for each configuration.

Robustness: Parametric studies showed that reducing club speed from 41 to 40 m/s caused the solver to compensate by increasing launch angle, demonstrating the model’s ability to adapt to parameter variations while maintaining near-optimal performance.

Conclusion

This project strengthened my skills in nonlinear optimization, stochastic modeling, and physics-based simulation. The experience of formulating real-world decision-making under uncertainty as an optimization problem—with careful attention to constraint formulation, objective function smoothness, and solver selection—highlighted how optimization techniques can address problems where inherent variability and environmental constraints must be accounted for.

Key learnings included constructing smooth objective functions from discrete data using cubic spline interpolation, handling non-convex optimization landscapes with multi-start approaches, and analyzing solution optimality through KKT conditions and Lagrange multipliers. The sensitivity analysis demonstrated how active constraints limit performance and how optimizers compensate when parameters change. More broadly, the project illustrated that accounting for systematic execution biases can significantly improve expected outcomes compared to naive strategies—a principle applicable to any domain where agents must optimize actions given uncertainty.